| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 오블완
- 티스토리챌린지
- conda base 기본 설정
- time wait port kill
- window netstat time wait 제거
- 3000 port kill
- conda 기초 설정
- 실행중인 포트 죽이기
- conda 가상환경 설정 오류
- conda base 활성화
- 려려
- Today
- Total
모도리는 공부중
21.03.09. 딥러닝 - RNN, LSTM, 단어 임베딩 본문
21.03.09. 딥러닝 - RNN, LSTM, 단어 임베딩
공부하는 모도리 2021. 3. 9. 18:08저번 시간 복습중..
21.03.08. 딥러닝 - RNN 단어 철자 예측 및 뉴스기사 데이터 실습
cnn은 차원이 고차원데이터가 되더라도 학습이 가능하다. 이유는 무얼까? cnn은 특징을 추출해주는 레이어이다. cnn을 붙여서 활용할 수 있는 데이터는 이미지에 국한되지 않는다. 글씨, 소리 등에
studying-modory.tistory.com
현재 데이터와 과거 데이터가 같이 들어와서 연산을 하기 때문에 빙글빙글 도는 것이 순환하는 것과 같다고 하여 RNN이라고 부른다.

선형회귀의 경우 3시간을 공부하면 30, 8시간을 공부하면 80점을 맞을거야 라는 예측값이라면, 선형분류는 동그라미와 세모를 분류하는 결정경계이다. 현재는 직선 하나로 분류할 수 있는 이진분류이지만 만약 여기에 다른게 늘어난다면?

다중분류가 된다. 다중분류가 되면 직선 하나만 가지고는 분류를 할 수가 없다. 그럼 어떻게 해야할까? 선을 하나 더 늘리면 된다.

동그라미냐 아니냐, 세모냐 아니냐, 별이냐 아니냐의 경계를 짓는 선을 하나씩 긋는다. 이처럼 다중분류는 각 범주마다 해당 범주냐 아니냐를 구분하는 여러 개의 선을 그어서 학습을 진행한다. 다중분류일 때는 선형모델이 범주 개수만큼 필요해진다.
분류는 양쪽 끝에 있는 데이터들은 나누기가 쉽다. 하지만 중요한건 가운데 경계에 있는 것이다. 이 경계에 있는 데이터를 얼마나 잘 나눠주느냐에 따라 데이터의 성능이 결정된다. 삶속에서도 극단적이지 않은, 애매한 상황에서의 결과를 내리는 것이 원래 제일 어려운 것처럼 데이터도 애매하면 나누기가 어렵다. 직선 가까이에 있는 데이터들은 결과는 나오지만 확실하다고 말하기가 어렵다. 선에 얼마나 가까이 있는지 멀리 있는지로 불확실성을 나눌 수 있다.

분홍색 동그라미를 기준으로 보자. 빨간색 선 입장, 파란색 선 입장, 초록색 선 입장에서 떨어진 거리에 따라 확신도가 달라진다. 선에서 멀리 떨어질수록 이것이 아닐거라는 확신도가 높아지며 가까울수록 확신도가 떨어진다. 고로, 위 그림에서는 초록색 선이 제일 가까운 동그라미는 세모가 아니라고 할 수 있는 확신도가 떨어지는 상황이므로 세모일 확률이 높아진다.
RNN층 같은 경우 은닉층을 여러개 못 쌓나요?라는 질문이 어제 들어왔었다. 은닉층을 여러개 쌓는다고 해서 성능이 뛰어나지지는 않지만 그 방법을 설명해보고자 한다.
return_sequences
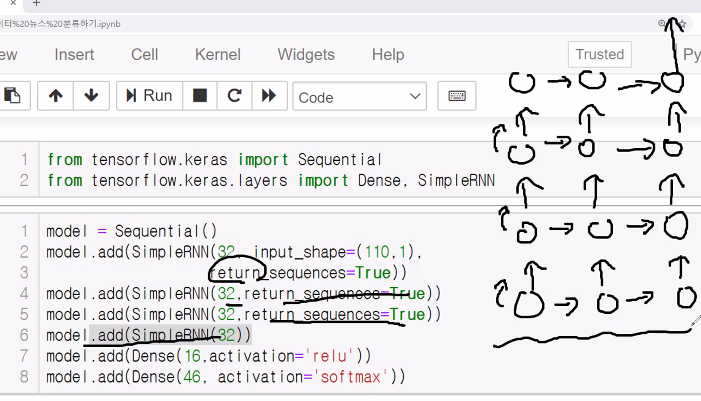
시간 개념 때문에 생긴 부분으로 과거 데이터를 같이 전달할 것인지 아니면 결과만 전달할 것인지를 결정하는 시스템이다. return_sequences를 안하게 되면 인코더 디코더처럼 층을 쌓는 구조가 된다.

위 그림처럼 서로 과거의 시간을 공유하지 않는 형태로 연결되는 구조로 만들어진다. 하지만 과거의 시간을 서로 공유하는 형태로 만들어야 한다면 return_sequences=True 형태로 만들어주면 된다. 이 형태로 만들게 되면 밑에 있는 RNN층과 위에 있는 RNN층은 서로의 시간을 공유하는 하나의 덩어리가 된다.
과거를 같이 고민할 수 있도록 층을 두텁게 쌓아주는 것이 일반적으로 층을 쌓아주는 구조라고 할 수 있다.
첫번째 층을 쌓고 나서 return_sequences를 넣게 되면 과거로부터의 연산을 같이 공유하며 나아가고, 마지막층은 return_sequences를 넣지 않아야 최종적으로 마무리를 지을 수 있다(?)

인코더에게 결과를 받아서 디코더도 따로 층을 또 쌓아서 해결할 수 있다.
어제 수업한 파일을 실행하여 22번째 셀에 있는 신경망층 코드를 다음과 같이 수정하고 모든 셀을 다시 실행해본다.
model = Sequential()
model.add(SimpleRNN(32, input_shape=(110, 1),
return_sequences=True))
# return_sequences=True는
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32, return_sequences=True))
model.add(SimpleRNN(32))
model.add(Dense(16, activation='relu'))
model.add(Dense(46, activation='softmax'))학습을 시키면 40퍼센트 대까지 올라간 것을 볼 수 있다.
| Train on 7185 samples, validate on 1797 samples Epoch 1/50 7185/7185 [==============================] - 30s 4ms/sample - loss: 2.7231 - accuracy: 0.3407 - val_loss: 2.4301 - val_accuracy: 0.3450 Epoch 2/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3906 - accuracy: 0.3571 - val_loss: 2.4137 - val_accuracy: 0.3450 Epoch 3/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.4082 - accuracy: 0.3534 - val_loss: 2.4087 - val_accuracy: 0.3450 Epoch 4/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.4042 - accuracy: 0.3534 - val_loss: 2.4033 - val_accuracy: 0.3450 Epoch 5/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3936 - accuracy: 0.3534 - val_loss: 2.3805 - val_accuracy: 0.3450 Epoch 6/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3571 - accuracy: 0.3648 - val_loss: 2.3013 - val_accuracy: 0.3812 Epoch 7/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3245 - accuracy: 0.3915 - val_loss: 2.4133 - val_accuracy: 0.3450 Epoch 8/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3873 - accuracy: 0.3556 - val_loss: 2.3584 - val_accuracy: 0.3545 Epoch 9/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3134 - accuracy: 0.3798 - val_loss: 2.4924 - val_accuracy: 0.2287 Epoch 10/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3595 - accuracy: 0.3548 - val_loss: 2.3363 - val_accuracy: 0.3567 Epoch 11/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3101 - accuracy: 0.3727 - val_loss: 2.3144 - val_accuracy: 0.3606 Epoch 12/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2859 - accuracy: 0.3705 - val_loss: 2.2883 - val_accuracy: 0.3578 Epoch 13/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2722 - accuracy: 0.3751 - val_loss: 2.2876 - val_accuracy: 0.3523 Epoch 14/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2522 - accuracy: 0.3820 - val_loss: 2.2388 - val_accuracy: 0.3996 Epoch 15/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2991 - accuracy: 0.3869 - val_loss: 2.1964 - val_accuracy: 0.4162 Epoch 16/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2846 - accuracy: 0.3900 - val_loss: 2.3592 - val_accuracy: 0.3456 Epoch 17/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3149 - accuracy: 0.3678 - val_loss: 2.3091 - val_accuracy: 0.3667 Epoch 18/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2786 - accuracy: 0.3761 - val_loss: 2.2885 - val_accuracy: 0.3612 Epoch 19/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2695 - accuracy: 0.3804 - val_loss: 2.2799 - val_accuracy: 0.3656 Epoch 20/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2609 - accuracy: 0.3788 - val_loss: 2.2800 - val_accuracy: 0.3701 Epoch 21/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2585 - accuracy: 0.3841 - val_loss: 2.2743 - val_accuracy: 0.3706 Epoch 22/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2586 - accuracy: 0.3900 - val_loss: 2.2858 - val_accuracy: 0.3639 Epoch 23/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2542 - accuracy: 0.3807 - val_loss: 2.2647 - val_accuracy: 0.3723 Epoch 24/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.2460 - accuracy: 0.3864 - val_loss: 2.2698 - val_accuracy: 0.3639 Epoch 25/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2504 - accuracy: 0.3805 - val_loss: 2.2851 - val_accuracy: 0.3689 Epoch 26/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.2470 - accuracy: 0.3775 - val_loss: 2.2690 - val_accuracy: 0.3701 Epoch 27/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.2370 - accuracy: 0.3926 - val_loss: 2.2694 - val_accuracy: 0.3695 Epoch 28/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.2328 - accuracy: 0.3958 - val_loss: 2.2606 - val_accuracy: 0.3656 Epoch 29/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2266 - accuracy: 0.3967 - val_loss: 2.2633 - val_accuracy: 0.3834 Epoch 30/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2156 - accuracy: 0.4038 - val_loss: 2.2405 - val_accuracy: 0.3901 Epoch 31/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2062 - accuracy: 0.4045 - val_loss: 2.2462 - val_accuracy: 0.3801 Epoch 32/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.1979 - accuracy: 0.4131 - val_loss: 2.2527 - val_accuracy: 0.3751 Epoch 33/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2197 - accuracy: 0.4213 - val_loss: 2.1514 - val_accuracy: 0.4452 Epoch 34/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.3148 - accuracy: 0.3665 - val_loss: 2.2775 - val_accuracy: 0.3745 Epoch 35/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2566 - accuracy: 0.3819 - val_loss: 2.3020 - val_accuracy: 0.3667 Epoch 36/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2285 - accuracy: 0.3808 - val_loss: 2.2344 - val_accuracy: 0.3767 Epoch 37/50 7185/7185 [==============================] - 28s 4ms/sample - loss: 2.2165 - accuracy: 0.3866 - val_loss: 2.2313 - val_accuracy: 0.3829 Epoch 38/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2061 - accuracy: 0.3904 - val_loss: 2.2422 - val_accuracy: 0.3868 Epoch 39/50 7185/7185 [==============================] - 26s 4ms/sample - loss: 2.3537 - accuracy: 0.3641 - val_loss: 2.3783 - val_accuracy: 0.3573 Epoch 40/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.3465 - accuracy: 0.3644 - val_loss: 2.3179 - val_accuracy: 0.3612 Epoch 41/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2457 - accuracy: 0.3858 - val_loss: 2.2558 - val_accuracy: 0.3806 Epoch 42/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2173 - accuracy: 0.3912 - val_loss: 2.2479 - val_accuracy: 0.3823 Epoch 43/50 7185/7185 [==============================] - 26s 4ms/sample - loss: 2.2057 - accuracy: 0.3964 - val_loss: 2.3467 - val_accuracy: 0.3751 Epoch 44/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.1982 - accuracy: 0.4035 - val_loss: 2.2180 - val_accuracy: 0.4046 Epoch 45/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2144 - accuracy: 0.3944 - val_loss: 2.2294 - val_accuracy: 0.3884 Epoch 46/50 7185/7185 [==============================] - 26s 4ms/sample - loss: 2.2473 - accuracy: 0.3869 - val_loss: 2.2729 - val_accuracy: 0.3762 Epoch 47/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2528 - accuracy: 0.3880 - val_loss: 2.2552 - val_accuracy: 0.3795 Epoch 48/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2038 - accuracy: 0.4136 - val_loss: 2.2940 - val_accuracy: 0.3884 Epoch 49/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.2040 - accuracy: 0.4109 - val_loss: 2.2138 - val_accuracy: 0.4146 Epoch 50/50 7185/7185 [==============================] - 27s 4ms/sample - loss: 2.1878 - accuracy: 0.4184 - val_loss: 2.2365 - val_accuracy: 0.4040 |

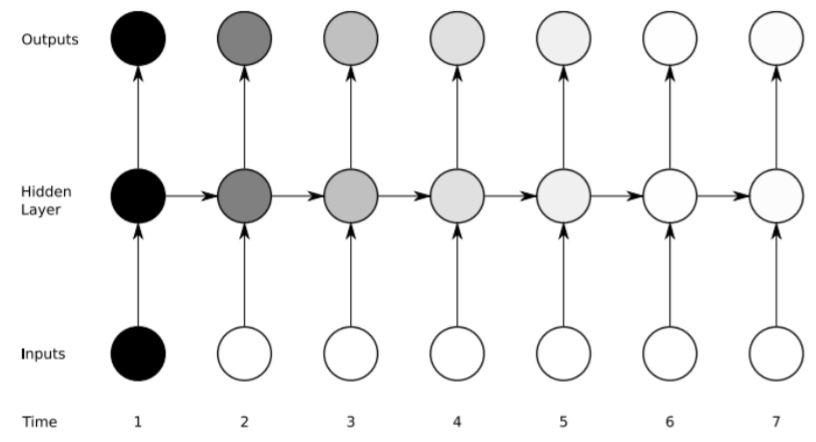
문장은 직전에 있는 것만 영향을 주는 것이 아니라 저 멀리에 있는 것도 영향을 줄 수 있다. 문장이 길어지기 시작하면 다른 글자들을 만나면서부터 점점 데이터가 길어지면서 목적성을 띄는 단어가 멀리 있을수록 학습이 제대로 되지 않는 문제가 발생하게 된다. Vanishing gradient도 마찬가지이다.
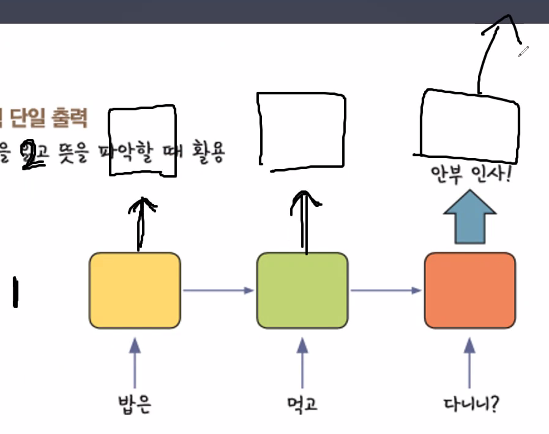
소실 문제 (Vanishing Gradient) - 시간이 지나면 이전의 입력값을 잊어버리게 된다.
LSTM (Long Short Term Memory)
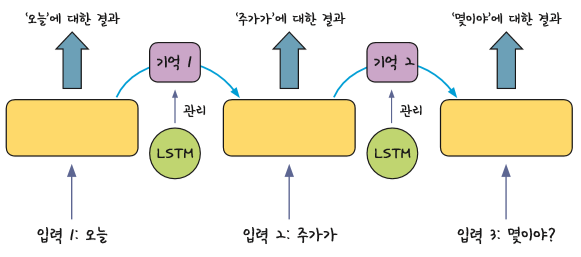
시간이 오래 지나면 점점 희석이 되는 부분을 좀 더 멀리까지 갈 수 있도록 관리해주는 기능이 추가된 것이 바로 LSTM이다. 중요한 부분의 기억값은 가중치를 높이고 강조하면서 유지될 수 있도록 관리하고 중요치 않은 기억값은 삭제시키거나 가중치를 낮추면서 연산해준다.
우리가 어제 배운 SimpleRNN은 바로바로 연산하는 방식이었다면 오늘 배울 LSTM은 과거 데이터를 계속 가져가기 때문에 조금 더 효과적인 결과값을 얻을 수 있다. LSTM을 사용하는 방법은 굉장히 쉽다. 어제 모델링했던 부분에서 SimpleRNN 부분을 LSTM으로 추가하고 변경만 해주면 된다. LSTM을 하게 되면 연산하는 양이 훨씬 많아지기 때문에 시간이 오래 걸리고 과대적합에 걸릴 확률도 올라간다. 그런 부분을 해결하기 위해 Dropout을 추가해도 좋다.
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, SimpleRNN, LSTMmodel = Sequential()
model.add(LSTM(32, input_shape=(110, 1),
return_sequences=True))
# return_sequences=True는
model.add(LSTM(32, return_sequences=True))
model.add(LSTM(32, return_sequences=True))
model.add(LSTM(32))
model.add(Dense(16, activation='relu'))
model.add(Dense(46, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='Adam', metrics=['accuracy'])
history = model.fit(X_train_pad_reshape, y_train_one_hot, validation_split=0.2, epochs=50)| Train on 7185 samples, validate on 1797 samples Epoch 1/50 7185/7185 [==============================] - 10s 1ms/sample - loss: 2.6739 - accuracy: 0.3003 - val_loss: 2.4146 - val_accuracy: 0.3450 Epoch 2/50 7185/7185 [==============================] - 3s 460us/sample - loss: 2.4039 - accuracy: 0.3534 - val_loss: 2.3510 - val_accuracy: 0.3450 Epoch 3/50 7185/7185 [==============================] - 3s 458us/sample - loss: 2.2705 - accuracy: 0.3992 - val_loss: 2.1794 - val_accuracy: 0.4613 Epoch 4/50 7185/7185 [==============================] - 3s 455us/sample - loss: 2.1569 - accuracy: 0.4451 - val_loss: 2.1273 - val_accuracy: 0.4558 Epoch 5/50 7185/7185 [==============================] - 3s 461us/sample - loss: 2.1189 - accuracy: 0.4582 - val_loss: 2.1123 - val_accuracy: 0.4636 Epoch 6/50 7185/7185 [==============================] - 3s 460us/sample - loss: 2.1498 - accuracy: 0.4362 - val_loss: 2.1191 - val_accuracy: 0.4469 Epoch 7/50 7185/7185 [==============================] - 3s 461us/sample - loss: 2.1082 - accuracy: 0.4571 - val_loss: 2.1230 - val_accuracy: 0.4374 Epoch 8/50 7185/7185 [==============================] - 3s 463us/sample - loss: 2.1026 - accuracy: 0.4554 - val_loss: 2.0991 - val_accuracy: 0.4641 Epoch 9/50 7185/7185 [==============================] - 3s 470us/sample - loss: 2.0919 - accuracy: 0.4622 - val_loss: 2.0960 - val_accuracy: 0.4496 Epoch 10/50 7185/7185 [==============================] - 3s 474us/sample - loss: 2.0939 - accuracy: 0.4603 - val_loss: 2.0994 - val_accuracy: 0.4530 Epoch 11/50 7185/7185 [==============================] - 3s 462us/sample - loss: 2.0990 - accuracy: 0.4564 - val_loss: 2.0886 - val_accuracy: 0.4647 Epoch 12/50 7185/7185 [==============================] - 3s 472us/sample - loss: 2.1033 - accuracy: 0.4589 - val_loss: 2.1230 - val_accuracy: 0.4418 Epoch 13/50 7185/7185 [==============================] - 3s 468us/sample - loss: 2.0945 - accuracy: 0.4617 - val_loss: 2.0851 - val_accuracy: 0.4636 Epoch 14/50 7185/7185 [==============================] - 3s 464us/sample - loss: 2.0905 - accuracy: 0.4594 - val_loss: 2.0787 - val_accuracy: 0.4658 Epoch 15/50 7185/7185 [==============================] - 3s 469us/sample - loss: 2.0784 - accuracy: 0.4657 - val_loss: 2.0817 - val_accuracy: 0.4674 Epoch 16/50 7185/7185 [==============================] - 4s 491us/sample - loss: 2.0783 - accuracy: 0.4664 - val_loss: 2.0929 - val_accuracy: 0.4669 Epoch 17/50 7185/7185 [==============================] - 3s 469us/sample - loss: 2.0693 - accuracy: 0.4686 - val_loss: 2.0824 - val_accuracy: 0.4647 Epoch 18/50 7185/7185 [==============================] - 3s 478us/sample - loss: 2.0681 - accuracy: 0.4678 - val_loss: 2.0705 - val_accuracy: 0.4702 Epoch 19/50 7185/7185 [==============================] - 4s 496us/sample - loss: 2.0641 - accuracy: 0.4699 - val_loss: 2.0697 - val_accuracy: 0.4686 Epoch 20/50 7185/7185 [==============================] - 3s 471us/sample - loss: 2.0625 - accuracy: 0.4686 - val_loss: 2.0681 - val_accuracy: 0.4697 Epoch 21/50 7185/7185 [==============================] - 3s 469us/sample - loss: 2.0567 - accuracy: 0.4707 - val_loss: 2.0724 - val_accuracy: 0.4730 Epoch 22/50 7185/7185 [==============================] - 3s 467us/sample - loss: 2.0600 - accuracy: 0.4699 - val_loss: 2.0675 - val_accuracy: 0.4725 Epoch 23/50 7185/7185 [==============================] - 3s 467us/sample - loss: 2.0608 - accuracy: 0.4678 - val_loss: 2.0743 - val_accuracy: 0.4697 Epoch 24/50 7185/7185 [==============================] - 3s 471us/sample - loss: 2.0604 - accuracy: 0.4669 - val_loss: 2.0603 - val_accuracy: 0.4691 Epoch 25/50 7185/7185 [==============================] - 3s 458us/sample - loss: 2.0513 - accuracy: 0.4679 - val_loss: 2.0669 - val_accuracy: 0.4736 Epoch 26/50 7185/7185 [==============================] - 3s 474us/sample - loss: 2.0462 - accuracy: 0.4711 - val_loss: 2.0523 - val_accuracy: 0.4741 Epoch 27/50 7185/7185 [==============================] - 3s 472us/sample - loss: 2.0450 - accuracy: 0.4704 - val_loss: 2.0507 - val_accuracy: 0.4697 Epoch 28/50 7185/7185 [==============================] - 3s 470us/sample - loss: 2.0366 - accuracy: 0.4671 - val_loss: 2.0327 - val_accuracy: 0.4725 Epoch 29/50 7185/7185 [==============================] - 3s 470us/sample - loss: 2.0224 - accuracy: 0.4695 - val_loss: 2.0385 - val_accuracy: 0.4608 Epoch 30/50 7185/7185 [==============================] - 3s 469us/sample - loss: 2.0217 - accuracy: 0.4678 - val_loss: 2.0202 - val_accuracy: 0.4819 Epoch 31/50 7185/7185 [==============================] - 4s 493us/sample - loss: 2.0015 - accuracy: 0.4828 - val_loss: 2.0123 - val_accuracy: 0.4825 Epoch 32/50 7185/7185 [==============================] - 4s 500us/sample - loss: 2.0081 - accuracy: 0.4832 - val_loss: 2.0511 - val_accuracy: 0.4725 Epoch 33/50 7185/7185 [==============================] - 3s 483us/sample - loss: 2.0055 - accuracy: 0.4852 - val_loss: 2.0090 - val_accuracy: 0.4752 Epoch 34/50 7185/7185 [==============================] - 3s 477us/sample - loss: 1.9773 - accuracy: 0.4888 - val_loss: 2.0025 - val_accuracy: 0.4791 Epoch 35/50 7185/7185 [==============================] - 3s 472us/sample - loss: 1.9744 - accuracy: 0.4895 - val_loss: 1.9842 - val_accuracy: 0.4814 Epoch 36/50 7185/7185 [==============================] - 3s 470us/sample - loss: 1.9783 - accuracy: 0.4875 - val_loss: 2.0103 - val_accuracy: 0.4719 Epoch 37/50 7185/7185 [==============================] - 3s 470us/sample - loss: 1.9845 - accuracy: 0.4863 - val_loss: 1.9890 - val_accuracy: 0.4814 Epoch 38/50 7185/7185 [==============================] - 3s 476us/sample - loss: 1.9703 - accuracy: 0.4885 - val_loss: 2.0018 - val_accuracy: 0.4786 Epoch 39/50 7185/7185 [==============================] - 3s 466us/sample - loss: 1.9702 - accuracy: 0.4878 - val_loss: 1.9874 - val_accuracy: 0.4864 Epoch 40/50 7185/7185 [==============================] - 3s 461us/sample - loss: 1.9592 - accuracy: 0.4905 - val_loss: 1.9835 - val_accuracy: 0.4880 Epoch 41/50 7185/7185 [==============================] - 3s 474us/sample - loss: 1.9585 - accuracy: 0.4939 - val_loss: 1.9932 - val_accuracy: 0.4925 Epoch 42/50 7185/7185 [==============================] - 3s 468us/sample - loss: 1.9452 - accuracy: 0.4949 - val_loss: 1.9915 - val_accuracy: 0.4891 Epoch 43/50 7185/7185 [==============================] - 3s 472us/sample - loss: 1.9505 - accuracy: 0.4894 - val_loss: 1.9718 - val_accuracy: 0.4897 Epoch 44/50 7185/7185 [==============================] - 3s 474us/sample - loss: 1.9453 - accuracy: 0.4923 - val_loss: 1.9680 - val_accuracy: 0.4841 Epoch 45/50 7185/7185 [==============================] - 3s 472us/sample - loss: 1.9376 - accuracy: 0.4903 - val_loss: 1.9689 - val_accuracy: 0.4847 Epoch 46/50 7185/7185 [==============================] - 3s 475us/sample - loss: 1.9357 - accuracy: 0.4926 - val_loss: 1.9774 - val_accuracy: 0.4858 Epoch 47/50 7185/7185 [==============================] - 3s 477us/sample - loss: 1.9389 - accuracy: 0.4938 - val_loss: 1.9633 - val_accuracy: 0.4880 Epoch 48/50 7185/7185 [==============================] - 4s 490us/sample - loss: 1.9300 - accuracy: 0.4937 - val_loss: 1.9716 - val_accuracy: 0.4936 Epoch 49/50 7185/7185 [==============================] - 3s 474us/sample - loss: 1.9443 - accuracy: 0.4906 - val_loss: 1.9688 - val_accuracy: 0.4947 Epoch 50/50 7185/7185 [==============================] - 3s 474us/sample - loss: 1.9298 - accuracy: 0.4935 - val_loss: 1.9882 - val_accuracy: 0.4869 |
plt.figure(figsize=(10, 5))
plt.plot(history.history['val_loss'], label='val_loss')
plt.plot(history.history['loss'], label='loss')
plt.legend()
plt.show()
plt.figure(figsize=(10, 5))
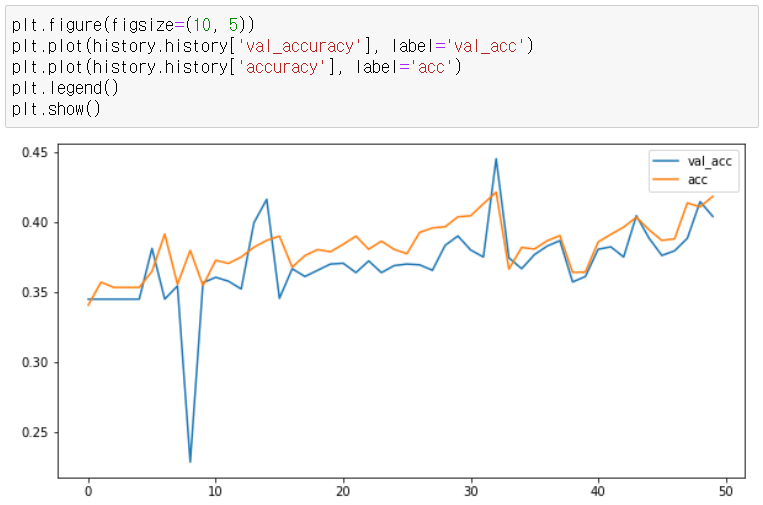
plt.plot(history.history['val_accuracy'], label='val_acc')
plt.plot(history.history['accuracy'], label='acc')
plt.legend()
plt.show()
LSTM을 사용하면 이처럼 결과값이 더 좋아지므로 앞으로 RNN을 사용할 때는 LSTM도 같이 쓴다고 생각하면 좋다. 그리고 LSTM과 같이 대표적으로 많이 사용되는 것이 있는데 바로 GRU이다. 기억을 관리하는 능력은 가져가면서 연산을 좀더 쉽게 할 수 있도록 만들어진 것이 바로 GRU이다. 여러가지 복잡한 연산과정을 간결화시킨 것으로 우리나라 교수님이 직접 만드셨다고 한다. LSTM과 GRU 둘 중에 그럼 어느 것이 더 좋느냐고 물어본다면 이건 서로 장단점이 다르기에 어느게 좋다고 할 수 없다. 데이터 양이 많고 더 좋은 결과를 보고자 한다면 LSTM, 데이터양이 적어서 간결하고 빠르게 하고 싶다면 GRU를 사용하면 좋다. 각각의 장단점이 다르므로 내가 쓰고자 하는 것에 맞춰서 잘 골라 사용하면 된다.
단어 임베딩 활용하기
원핫인코딩을 하게 되면 내가 가지고 있는 단어 길이에 따라 크기가 달라질 수 있다. 그 말은 즉슨 단어 사전에 따라 데이터 크기가 달라지게 된다는 것이다. 단어사전을 표현하기 위해 BOG했던 것처럼 원핫인코딩도 내가 필요한 단어사전을 표현하기 위해 원핫인코딩을 하게 되면 한 개의 단어를 표현할 때 숫자가 매우 많이 필요해지게 된다. 만약 5000개의 단어를 가진 단어사전이라면 어느 단어 하나를 표현하기 위해 5000개의 숫자가 나타날 것이다. 이게 첫 번째 단점이다.

두 번째 단점은 원핫인코딩은 각각의 단어를 구분하는 용도 말고는 추가적인 정보를 얻을 수 없다. 단순하게 단어를 구분하고 학습하는 정도일 뿐이다.

하지만 우리에겐 단어별로 숫자를 다르게 매겨서 구분할 수 있는 것이 필요하다.

라벨 인코딩은 단어를 빈도 숫자로만 표현하기 때문에 단순하다. 이것만 가지고도 문장을 이해할 수는 있지만 우리가 원하는 결과값을 뽑아내기는 어렵다. 이런 문제들 때문에 우리가 원하는 결과값을 뽑아내기 위해 나온 것이 바로 word embedding이다. 개, 고양이, 사자를 임배딩하기 위해 초반에는 랜덤한 숫자를 집어넣는다. 서로 어떤 관계를 가지고 있는지 모르므로 일단 처음에는 임의의 숫자를 넣고 학습을 통해 이 숫자들을 조정한다. 임배딩은 학습할 때 같이 언급되는 것들을 보면서 비슷한 숫자를 매기게 된다. 자주 언급되는 빈도수에 따라 비슷한 숫자끼리도 값을 조정해주고 같이 언급되지 않으면 숫자 패턴을 다르게 매겨주면서 학습할 때 값을 계속 조정할 것이다.
이전에 돌렸던 과정을 다시 돌리는데 몇가지 코드만 수정을 가해준다. 다음은 코드를 그대로 쭉 나열한 것인데 수정이 된 코드가 있는 셀은 바로 보이고 수정되지 않은 셀은 더보기란에 가려주었다.
from tensorflow.keras.datasets import reuters
import numpy as np
import matplotlib.pyplot as plt
(X_train, y_train), (X_test, y_test) = reuters.load_data(num_words=1000)
# num_words=1000 : 빈도가 높은 1000개만 남기고 나머지는 다 oov_char=2 기능이 적용되어 2로 바뀐다.
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)out : (8982,) (8982,) (2246,) (2246,)
필요치 않은 부분은 제외
# 정답데이터 개수 확인
np.unique(y_train) # 뉴스 주제 개수 알아보기 (46가지 확인)
# RNN을 활용하면 뉴스에 등장하는 단어의 순서도 중요해진다.out :
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45], dtype=int64)
# 뉴스 기사들의 길이 계산
train_len = [ len(doc) for doc in X_train ]
print("최대값 : ", max(train_len))
print("최소값 : ", min(train_len))
print("평균값 : ", np.mean(train_len))
print("중앙값 : ", np.median(train_len))out : 최대값 : 2376 최소값 : 13 평균값 : 145.5398574927633 중앙값 : 95.0
plt.hist(train_len, bins=20)
plt.show()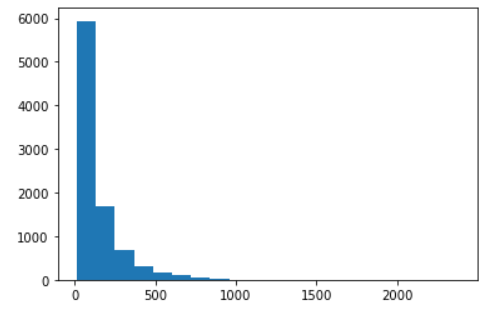
from tensorflow.keras.preprocessing import sequence # 시퀀스 길이 맞추는 용도
from tensorflow.keras.utils import to_categorical # 정답 → 확률 정보 변경
X_train_pad = sequence.pad_sequences(X_train, maxlen=110)
X_test_pad = sequence.pad_sequences(X_test, maxlen=110)
# sample은 8982개, 길이(time steps)는 110개
X_train_pad.shapeout : (8982, 110)
X_train_pad_reshape = X_train_pad.reshape(X_train_pad.shape[0], # 8982
X_train_pad.shape[1], # 110
1)
X_test_pad_reshape = X_test_pad.reshape(X_test_pad.shape[0], # 2246
X_test_pad.shape[1], # 110
1)
print(X_train_pad_reshape.shape)
print(X_test_pad_reshape.shape)out :
(8982, 110, 1)
(2246, 110, 1)
y_train_one_hot = to_categorical(y_train)
y_test_one_hot = to_categorical(y_test)from tensorflow.keras.layers import Embedding, Dropout
# 다시 2차원으로 변경
X_train_pad_reshape = X_train_pad_reshape.reshape(8982, 110)
X_test_pad_reshape = X_test_pad_reshape.reshape(2246, 110)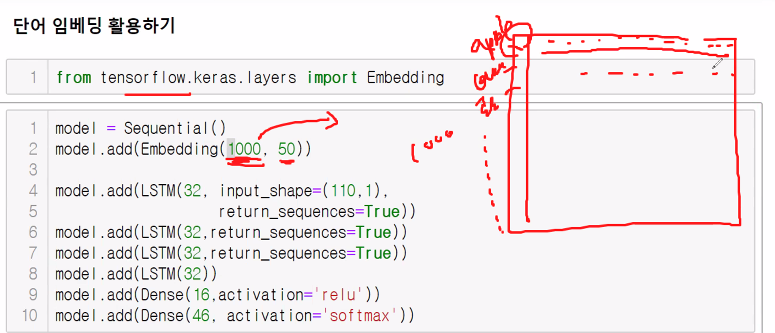
-
model.add(Embedding(전체 단어의 수, 각 단어를 표현하기 위한 숫자 갯수))
-
각 단어를 표현하기 위한 숫자 갯수는 크면 클수록 관계 사이를 풍부하게 표현해준다.
-
너무 적게 적으면 단어를 구분하는 것과 크게 차이가 없을 수 있으며 많이 적으면 풍부할 수 있으나 그만큼 과대적합이 걸릴 수도 있다.
-
하지만 데이터를 불러올 때 num_words=1000를 설정하게 되면 신경망을 구성할 때 Embedding에서 데이터의 갯수가 한정되어 있으므로 학습과정에서 오차역전파를 통해 단어를 좀 더 깔끔하게 정리할 수 있다.
model = Sequential()
model.add(Embedding(1000, 50)) # 학습을 통해서 조절이 된다.
model.add(LSTM(32, return_sequences=True))
model.add(LSTM(64, return_sequences=True))
model.add(Dropout(0.25))
model.add(LSTM(128))
model.add(Dropout(0.25))
model.add(Dense(16, activation='relu'))
model.add(Dense(46, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='Adam', metrics=['accuracy'])
history = model.fit(X_train_pad_reshape, y_train_one_hot, validation_split=0.2, epochs=50)| Train on 7185 samples, validate on 1797 samples Epoch 1/50 7185/7185 [==============================] - 11s 2ms/sample - loss: 2.1475 - accuracy: 0.4448 - val_loss: 1.8638 - val_accuracy: 0.5159 Epoch 2/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.9728 - accuracy: 0.4786 - val_loss: 1.9226 - val_accuracy: 0.4847 Epoch 3/50 7185/7185 [==============================] - 6s 809us/sample - loss: 1.8633 - accuracy: 0.5152 - val_loss: 1.8126 - val_accuracy: 0.5314 Epoch 4/50 7185/7185 [==============================] - 6s 804us/sample - loss: 1.8297 - accuracy: 0.5144 - val_loss: 1.7419 - val_accuracy: 0.5487 Epoch 5/50 7185/7185 [==============================] - 6s 812us/sample - loss: 1.7194 - accuracy: 0.5521 - val_loss: 1.7135 - val_accuracy: 0.5470 Epoch 6/50 7185/7185 [==============================] - 6s 821us/sample - loss: 1.6842 - accuracy: 0.5627 - val_loss: 1.6749 - val_accuracy: 0.5643 Epoch 7/50 7185/7185 [==============================] - 6s 817us/sample - loss: 1.6480 - accuracy: 0.5715 - val_loss: 1.6556 - val_accuracy: 0.5754 Epoch 8/50 7185/7185 [==============================] - 6s 824us/sample - loss: 1.6372 - accuracy: 0.5776 - val_loss: 1.6695 - val_accuracy: 0.5737 Epoch 9/50 7185/7185 [==============================] - 6s 821us/sample - loss: 1.6365 - accuracy: 0.5726 - val_loss: 1.6448 - val_accuracy: 0.5776 Epoch 10/50 7185/7185 [==============================] - 6s 820us/sample - loss: 1.5948 - accuracy: 0.5833 - val_loss: 1.6286 - val_accuracy: 0.5704 Epoch 11/50 7185/7185 [==============================] - 6s 810us/sample - loss: 1.5808 - accuracy: 0.5900 - val_loss: 1.7857 - val_accuracy: 0.5259 Epoch 12/50 7185/7185 [==============================] - 6s 814us/sample - loss: 1.6586 - accuracy: 0.5768 - val_loss: 1.6545 - val_accuracy: 0.5760 Epoch 13/50 7185/7185 [==============================] - 6s 819us/sample - loss: 1.6450 - accuracy: 0.5846 - val_loss: 1.6150 - val_accuracy: 0.5826 Epoch 14/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.5665 - accuracy: 0.5942 - val_loss: 1.6382 - val_accuracy: 0.5882 Epoch 15/50 7185/7185 [==============================] - 6s 812us/sample - loss: 1.5458 - accuracy: 0.5989 - val_loss: 1.6076 - val_accuracy: 0.5854 Epoch 16/50 7185/7185 [==============================] - 6s 826us/sample - loss: 1.5026 - accuracy: 0.6067 - val_loss: 1.5866 - val_accuracy: 0.5932 Epoch 17/50 7185/7185 [==============================] - 6s 828us/sample - loss: 1.4911 - accuracy: 0.6093 - val_loss: 1.5728 - val_accuracy: 0.5988 Epoch 18/50 7185/7185 [==============================] - 6s 828us/sample - loss: 1.4874 - accuracy: 0.6156 - val_loss: 1.5845 - val_accuracy: 0.5965 Epoch 19/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.4577 - accuracy: 0.6199 - val_loss: 1.5525 - val_accuracy: 0.6099 Epoch 20/50 7185/7185 [==============================] - 6s 812us/sample - loss: 1.4290 - accuracy: 0.6308 - val_loss: 1.5369 - val_accuracy: 0.6194 Epoch 21/50 7185/7185 [==============================] - 6s 837us/sample - loss: 1.4354 - accuracy: 0.6267 - val_loss: 1.5433 - val_accuracy: 0.6099 Epoch 22/50 7185/7185 [==============================] - 6s 846us/sample - loss: 1.3993 - accuracy: 0.6335 - val_loss: 1.4920 - val_accuracy: 0.6283 Epoch 23/50 7185/7185 [==============================] - 6s 832us/sample - loss: 1.4447 - accuracy: 0.6303 - val_loss: 1.5213 - val_accuracy: 0.6244 Epoch 24/50 7185/7185 [==============================] - 6s 853us/sample - loss: 1.3955 - accuracy: 0.6358 - val_loss: 1.4941 - val_accuracy: 0.6233 Epoch 25/50 7185/7185 [==============================] - 6s 823us/sample - loss: 1.3275 - accuracy: 0.6516 - val_loss: 1.4995 - val_accuracy: 0.6311 Epoch 26/50 7185/7185 [==============================] - 6s 819us/sample - loss: 1.3123 - accuracy: 0.6566 - val_loss: 1.5409 - val_accuracy: 0.6288 Epoch 27/50 7185/7185 [==============================] - 6s 815us/sample - loss: 1.3232 - accuracy: 0.6554 - val_loss: 1.4897 - val_accuracy: 0.6322 Epoch 28/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.2822 - accuracy: 0.6664 - val_loss: 1.4762 - val_accuracy: 0.6305 Epoch 29/50 7185/7185 [==============================] - 6s 811us/sample - loss: 1.2602 - accuracy: 0.6671 - val_loss: 1.5058 - val_accuracy: 0.6183 Epoch 30/50 7185/7185 [==============================] - 6s 816us/sample - loss: 1.2269 - accuracy: 0.6706 - val_loss: 1.4926 - val_accuracy: 0.6372 Epoch 31/50 7185/7185 [==============================] - 6s 816us/sample - loss: 1.2215 - accuracy: 0.6763 - val_loss: 1.5168 - val_accuracy: 0.6338 Epoch 32/50 7185/7185 [==============================] - 6s 816us/sample - loss: 1.2456 - accuracy: 0.6697 - val_loss: 1.4718 - val_accuracy: 0.6188 Epoch 33/50 7185/7185 [==============================] - 6s 815us/sample - loss: 1.2292 - accuracy: 0.6703 - val_loss: 1.4672 - val_accuracy: 0.6444 Epoch 34/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.1601 - accuracy: 0.6856 - val_loss: 1.4944 - val_accuracy: 0.6516 Epoch 35/50 7185/7185 [==============================] - 6s 817us/sample - loss: 1.1581 - accuracy: 0.6864 - val_loss: 1.4419 - val_accuracy: 0.6505 Epoch 36/50 7185/7185 [==============================] - 6s 816us/sample - loss: 1.1314 - accuracy: 0.6944 - val_loss: 1.4297 - val_accuracy: 0.6477 Epoch 37/50 7185/7185 [==============================] - 6s 812us/sample - loss: 1.1371 - accuracy: 0.6953 - val_loss: 1.4502 - val_accuracy: 0.6372 Epoch 38/50 7185/7185 [==============================] - 6s 817us/sample - loss: 1.1452 - accuracy: 0.6928 - val_loss: 1.4568 - val_accuracy: 0.6494 Epoch 39/50 7185/7185 [==============================] - 6s 813us/sample - loss: 1.1232 - accuracy: 0.7006 - val_loss: 1.4436 - val_accuracy: 0.6572 Epoch 40/50 7185/7185 [==============================] - 6s 818us/sample - loss: 1.0884 - accuracy: 0.7102 - val_loss: 1.4379 - val_accuracy: 0.6633 Epoch 41/50 7185/7185 [==============================] - 6s 824us/sample - loss: 1.0556 - accuracy: 0.7219 - val_loss: 1.4180 - val_accuracy: 0.6633 Epoch 42/50 7185/7185 [==============================] - 6s 824us/sample - loss: 1.0340 - accuracy: 0.7269 - val_loss: 1.4453 - val_accuracy: 0.6644 Epoch 43/50 7185/7185 [==============================] - 6s 837us/sample - loss: 1.0219 - accuracy: 0.7339 - val_loss: 1.3730 - val_accuracy: 0.6722 Epoch 44/50 7185/7185 [==============================] - 6s 835us/sample - loss: 1.0277 - accuracy: 0.7344 - val_loss: 1.3886 - val_accuracy: 0.6800 Epoch 45/50 7185/7185 [==============================] - 6s 831us/sample - loss: 0.9926 - accuracy: 0.7403 - val_loss: 1.3978 - val_accuracy: 0.6528 Epoch 46/50 7185/7185 [==============================] - 6s 825us/sample - loss: 0.9768 - accuracy: 0.7389 - val_loss: 1.4106 - val_accuracy: 0.6683 Epoch 47/50 7185/7185 [==============================] - 6s 836us/sample - loss: 0.9684 - accuracy: 0.7461 - val_loss: 1.4137 - val_accuracy: 0.6761 Epoch 48/50 7185/7185 [==============================] - 6s 821us/sample - loss: 0.9726 - accuracy: 0.7402 - val_loss: 1.4178 - val_accuracy: 0.6639 Epoch 49/50 7185/7185 [==============================] - 6s 814us/sample - loss: 0.9293 - accuracy: 0.7552 - val_loss: 1.3859 - val_accuracy: 0.6900 Epoch 50/50 7185/7185 [==============================] - 6s 816us/sample - loss: 0.9100 - accuracy: 0.7598 - val_loss: 1.4021 - val_accuracy: 0.6583 |
plt.figure(figsize=(10, 5))
plt.plot(history.history['val_loss'], label='val_loss')
plt.plot(history.history['loss'], label='loss')
plt.legend()
plt.show()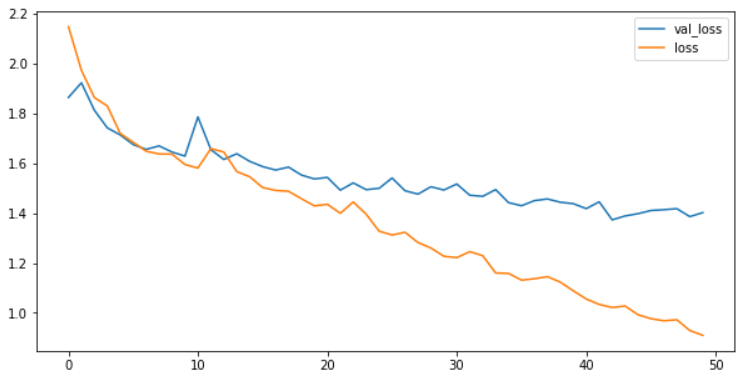
plt.figure(figsize=(10, 5))
plt.plot(history.history['val_accuracy'], label='val_acc')
plt.plot(history.history['accuracy'], label='acc')
plt.legend()
plt.show()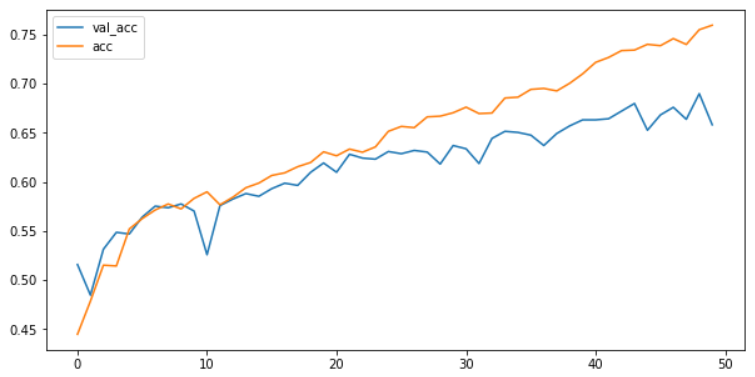
워드 임배딩에 대한 상세 설명 진행. (pdf 파일을 보면서 진행한다.)
- 자연어를 컴퓨터가 이해하고, 효율적으로 처리하기 위해서는 컴퓨터가 이해할 수 있도록 변환할 필요가 있다.
- 단어의 의미를 벡터화 하는 것을 워드 임베딩 이라 한다
- 주로 희소 표현 (one hot encoding) 에서 밀집 표현으로 변환하는 것을 의미
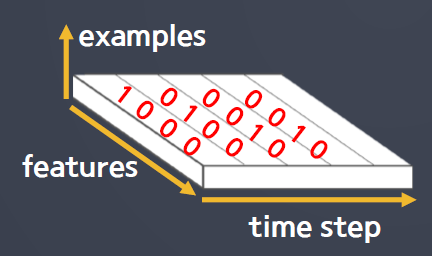

원핫인코딩을 진행하면 결과가 거의 다 0이 들어있고 실제 1이 들어있는 부분은 얼마 없다. 어떤 데이터든지 실제 의미가 있는 데이터는 드문드문 존재한다고 해서 sparse data라고 한다. 하지만 워드 임배딩을 하게 되면 단어가 몇개 있든지 내가 정해준 숫자 안에서 표현해야하므로 밀집된 형태의 숫자로 표현을 하게 된다.
- 단어를 밀집 벡터의 형태로 표현하는 방법을 워드 임베딩 (word embedding) 이라고 한다
- 임베딩 과정을 통해 나온 결과를 임베딩 벡터(embedding)라고 한다
- 워드 임베딩 방법론으로는 Word2Vec, FastText, Glove 등이 있다
- 케라스에도 제공하는 도구인 Embedding() 은 위에서 사용하는 방법과 다르게 랜덤한 값을 가지는 밀집 벡터로 변환한 뒤에, 인공 신경망의 가중치를 학습한다.
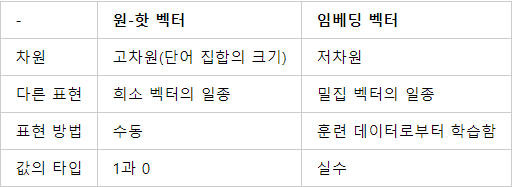
임베딩 벡터를 누가 미리 학습시켜놓은 것을 가져다가 사용할 수도 있다. 만약 우리가 8900개의 뉴스를 가지고 표현한 것보다 누군가가 1000개의 단어를 표현하기 위해 더 많은 데이터를 가지고 이미 만들어놓고 그것을 제공을 해준다? 그럼 그것을 가져다가 사용하는 것이 훨씬 더 효율적일 것이다.
영화데이터를 이용하여 학습을 진행해보자.
아래 링크를 눌러 접속하여 download zip을 받는다.
e9t/nsmc
Naver sentiment movie corpus. Contribute to e9t/nsmc development by creating an account on GitHub.
github.com

데이터를 받아준다.
import pandas as pd
train = pd.read_csv("data/nsmc-master/ratings_train.txt", delimiter="\t")
test = pd.read_csv("data/nsmc-master/ratings_test.txt", delimiter="\t")
train.shape, test.shapeout : ((150000, 3), (50000, 3))
train.head()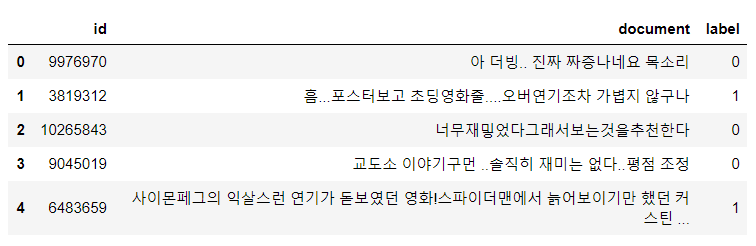
결측치 삭제
train.dropna(inplace=True)
test.dropna(inplace=True)
train.shape, test.shapeout : ((149995, 3), (49997, 3)
X_train = train['document']
X_test = test['document']
y_train = train['label']
y_test = test['label']
X_train.shape, X_test.shape, y_train.shape, y_test.shapeout : ((149995,), (49997,), (149995,), (49997,))
토큰화
- 텍스트를 단어 단위로 잘라주는 것을 일반적으로 많이 진행한다.
# 문장을 띄어쓰기 단위로 쪼개준다.
from tensorflow.keras.preprocessing.text import Tokenizer
# tokenizer를 불러올 때 그냥 Tokenizer()로 호출할 수도 있지만
# num_words=?를 통해 빈도 높은 단어를 몇개까지 불러올지 설정해줄 수 있다.
# 인덱스는 그대로 유지되지만 5000을 지정하게 되면 실제 바꿀 때 값은 5000위까지로 조정된다.
tokenizer = Tokenizer(num_words=5000)
# 빈도를 확인할 수 있다.
tokenizer.fit_on_texts(X_train) # 문장 토큰화 + 단어 빈도 측정
tokenizer.word_index


# 데이터 단어사전 개수 확인
len(tokenizer.word_index)out : 296310
# 단어별 실제 등장 빈도수
tokenizer.word_counts


데이터 변경(랭크 기준)
# 실제 텍스트 데이터를 랭킹 숫자로 라벨인코딩
X_train_seq = tokenizer.texts_to_sequences(X_train)
X_test_seq = tokenizer.texts_to_sequences(X_test)
X_train[0]out : '아 더빙.. 진짜 짜증나네요 목소리'
X_train_seq
num_words=5000를 토큰화에 넣기 전과 후의 데이터이다.

숙제
1. 시퀀스 길이 맞추기
2. 모델링
- LSTM
- Dropout
- Embedding
'K-디지털 빅데이터 분석서비스 개발자과정 20.11.02~21.04.12 > PYTHON(웹크롤링, 머신·딥러닝)' 카테고리의 다른 글
| 21.03.11. 딥러닝 - 시계열 RNN (4) | 2021.03.11 |
|---|---|
| 21.03.08. 딥러닝 - RNN 단어 철자 예측 및 뉴스기사 데이터 실습 (0) | 2021.03.08 |
| 21.03.05. 딥러닝 - 동물 이미지 인식, 패션 이미지 분류 (0) | 2021.03.05 |
| 21.03.04. 딥러닝 - (0) | 2021.03.04 |
| 21.03.03. 딥러닝 - 숫자손글씨 인식 마지막, 개고양이 인식 (1) | 2021.03.03 |




